Ⅰ. 서론
Sims(1980)의 벡터자기회귀(vector autoregressive, VAR) 모형이 도입된 이후 주택시장과 거시·금융시장 사이의 연관관계를 파악하기 위한 실증분석이 활발히 진행됐으며, 그동안 다양한 연구가 축적됐다. 일반적으로 시계열 자료들은 관측치의 주기(frequency)가 서로 다른 경우가 많아 VAR(또는 VECM) 모형으로 두 개 이상의 시계열 자료를 동시에 분석하기 위해서는 분석 대상 자료의 주기를 저빈도(low frequency) 자료의 주기에 통일시켜 분석을 수행한다. 예를 들어, 주택매매가격과 실질GDP와 같은 거시경제와의 연관성을 분석하는 경우 월별 자료인 주택매매가격을 분기자료로 변환한 다음 실질GDP와의 상호의존성을 파악한다(송인호, 2015; 전현진, 2023). 또 다른 예로 주택매매가격과 주식시장과의 관계를 분석하는 경우 일별로 관측되는 주가자료를 월별로 변환한 후 주택시장과 금융시장의 연관성을 분석했다(금기조·김병량, 2015; 신종협, 2019). 즉, 관측 주기가 다른 자료들 사이의 관계는 VAR 모형으로 직접 분석하기 어려워 고빈도(high frequency) 자료를 집계(aggregation)하여 저빈도 자료의 주기와 통일했는데, 이 경우 자료를 집계하는 과정에서 고빈도 자료가 갖고 있는 정보의 손실이 발생한다(Ghysels, 2016). 이러한 한계점을 보완하기 위해 Ghysels(2016)의 혼합주기(mixed frequency, MF) VAR 모형이 개발됐으며, MF-VAR 모형은 VAR 모형과 비교하여 정보의 손실이 발생하지 않고 예측성과도 우월한 것으로 알려졌다.
한편, 국내 주택시장은 불확실성 충격에 영향을 받아왔다. 대표적으로 1997~1998년에 발생한 외환위기, 2007~2009년에 발발한 글로벌 금융위기, 그리고 2020년도의 코로나19 위기 등의 영향을 받았다. Knight(1921)는 불확실성(uncertainty)을 사람들이 사건이 발생할 가능성을 예측할 수 없는 능력으로 정의했는데, 일반적으로 불확실성이 증가하면 거시경제를 비롯하여 주택시장에 부정적인 영향을 끼친다. 특히, 불확실성이 증가하면 가계는 내구재 소비를 연기하는 의사결정을 하여 경기가 침체되는 상황이 발생한다(Bloom, 2014). 아울러 이러한 불확실성은 금융시장에서도 발생하며 주택시장은 금융시스템과 밀접하게 연결되었기 때문에 금융불확실성의 변화는 주택수요나 대출 조건 등에 영향을 미치게 된다. 금융시장의 불확실성이 증가하여 금융기관들이 불확실성을 높게 인식할 경우 신용위험을 관리하기 위해 주택담보대출 기준을 강화할 수 있고, 이는 주택 구입비용 증가로 주택수요 감소로 이어지게 된다. 또한 금융불확실성의 증가가 경제 전반의 불확실성으로 이어지면 가계의 소득 전망에도 부정적인 영향을 미치고 되고 이로 인해 가계는 주택구매 결정을 연기하게 된다. 마지막으로 금융불확실성은 소비자의 심리적 요인에도 영향을 끼칠 수 있으며 금융시장의 불안정한 상황은 경제 전반에 부정적인 신호로 해석될 수 있다. 따라서 주택시장에서도 주택수요가 감소하고 주택가격이 하락할 수 있다. 이와 같이 금융시장의 불확실성은 주택시장과도 연계되어 있으므로 불확실성과 주택시장의 연관관계를 파악하는 것은 주택시장의 안정화를 위해 필수적이다. 이러한 측면을 고려하여 본 연구는 불확실성과 주택시장 사이의 연관관계를 분석한다.
최근 불확실성이 주택시장에 미치는 영향에 대한 실증연구가 진행됐는데, 본 연구는 기존 연구와 비교하여 다음과 같은 차별성이 있다. 첫째, 기존 연구 중 김지연 외(2020), 전지홍·조영석(2018), 최차순(2022) 등은 불확실성의 대리변수로 Baker et al.(2016)가 작성한 경제정책 불확실성(economic policy uncertatinty, EPU) 지수를 이용하고 VAR 모형으로 주택시장과의 연관관계를 분석했다. 반면, 본 연구는 불확실성의 대리변수로 고빈도 자료인 주식시장의 VKOSPI 지수(변동성 지수, volatility index of KOSPI200)를 이용한다.1) 이 경우 VKOSPI 지수는 일별로 관측되는 반면, 주택가격 자료는 월별로 발표되어 자료의 관측 주기가 불일치한 문제가 발생한다. 따라서 전통적인 VAR 모형으로는 분석이 불가능하며 VKOSPI 지수를 월별로 집계하여 자료의 주기를 통일해야 하는데, 해당자료를 월별로 집계하는 과정에서 정보의 손실이 발생한다. 본 연구에서는 고빈도 자료가 갖고 있는 정보의 손실을 최소화하기 위해 Ghysels(2016)의 MF-VAR 모형을 이용하여 충격반응 및 분산분해 등의 분석을 시행하고 고빈도 자료를 이용하는 경우 나타나는 특징을 분석한다.
둘째, Diebold and Yilmaz(2009, 2014)의 연계성(connectedness) 접근법을 이용하여 불확실성과 주택시장간 연관관계를 추가적으로 분석한다. 연계성 접근법은 분산분해 요소들을 이용하여 다양한 연계성 지표를 도출하고 이를 토대로 변수들 간의 파급효과의 크기를 측정할 수 있다. 또한, 파급효과의 동태적 추이를 분석할 수 있는 장점이 있어 해당 모형이 개발된 이후 널리 활용되는 모형이다. 이 때 전통적인 VAR 모형을 이용한 김지연 외(2020)의 연구와 달리 MF-VAR 모형을 연계성 접근법에 결합한 Cotter et al.(2023)의 실증분석 모형을 이용하고 전통적인 VAR 모형과 MF-VAR 모형의 추정결과가 어떻게 달라지는지 비교한다.
본 연구의 주요 분석결과는 다음과 같다. MF-VAR 모형을 이용한 충격반응함수 추정결과 금융불확실성 충격은 주택시장에 부정적인 영향을 미치는 것으로 분석됐으며, 해당 효과는 충격이 발생한 시점에 따라 이질적으로 나타났다. 다음으로 연계성 접근법을 이용한 결과 금융불확실성과 주택시장의 연계성은 글로벌 금융위기 및 코로나19 등 경제위기 기간에 높아지는 것으로 분석됐다. 또한, 금융불확실성은 주택시장에 지속적으로 영향을 미치는 순 전달자의 역할을 하는것으로 분석됐다. 마지막으로 MF-VAR 모형과 전통적인 VAR 모형으로 추정된 결과를 비교하면 전통적인 VAR 모형은 MF-VAR 모형과 비교하여 파급효과를 과소추정하는 것으로 나타났다.
본 논문의 구성은 다음과 같다. 제 II장에서는 본 연구와 관련된 해외 및 국내 선행연구들을 정리하고, 제 III장에서는 실증분석 모형에 대해 설명한다. 제 Ⅳ장에서는 본 연구에서 이용한 분석자료와 실증분석 결과에 대해 논의한다. 마지막으로 제 V장에서는 실증분석결과를 요약하고 결론을 제시한다.
II. 선행연구
글로벌 금융위기를 계기로 불확실성이 거시경제 및 금융시장에 얼마나 영향을 미치는가에 대한 연구가 다수 진행됐다. 이와 함께 불확실성이 주택시장에 미치는 영향을 분석한 실증연구도 활발히 진행되고 있는 상황이다. 이러한 연구를 진행할 때 불확실성의 대리변수로 주식시장에서 관찰되는 내재변동성(implied volatility), Jurado et al.(2015)의 거시경제 불확실성(macroeconomic uncertainty) 지수 또는 Baker et al.(2016)이 작성한 경제정책 불확실성 지수가 주로 이용된다.
본 논문과 관련된 선행연구는 크게 두 가지 범주로 정리할 수 있다. 첫 번째 범주는 불확실성과 주택시장 사이의 상호연관성을 분석한 연구이다. 두 번째 범주는 분석대상 자료의 주기가 일치하지 않는 경우 Ghysels(2016)의 MF-VAR 모형을 이용한 연구이다.
먼저, 불확실성과 주택시장의 연관성을 분석한 해외 연구는 다음과 같다. Antonakakis et al.(2015)은 미국의 불확실성지수와 주택가격 변동률 간 시간가변조건부상관계수(dynamic conditional correlation, DCC)를 측정한 결과 두 변수는 음의 상관관계를 갖고 시간에 따라 변동하는 것으로 분석했다. Thanh et al.(2020)은 미국의 부동산 불확실성지수를 새롭게 작성하고 해당 지수를 이용하여 미국 주택시장과의 연관관계를 분석했다. Christou et al.(2019)는 시간가변모수-요인활용다변수자기회귀모형(time-varying parameter VAR model, TVP-VAR)을 이용하여 불확실성 충격은 미국 주택시장에 부정적인 영향을 끼치며 충격의 크기는 시간에 따라 변동한다는 결과를 제시했다.
불확실성과 주택시장의 연관관계를 분석한 국내 연구들은 공통적으로 불확실성이 국내 주택시장에 영향을 미친다는 결과를 제시했다. 대표적으로 전지홍·조영석(2018)은 VECM을 이용하여 미국의 경제정책 불확실성이 상승하면 국내 주택매매가격지수 및 임대가격지수에 부정적인 영향을 끼치는 것으로 분석했다. 김지연 외(2020)는 Diebold and Yilmaz(2014)의 연계성 접근법을 이용하여 경제정책 불확실성과 주택 매매가격 변동률 사이의 연관관계를 분석하여 국내 경제정책 불확실성지수는 전국 및 지역별 주택 매매가격 변동률에 영향을 미친다는 결과를 제시했다. 최차순(2022)은 VECM을 이용하여 국내 경제정책 불확실성이 상승하면 주택매매가격, 주택전세가격, 토지가격에 부정적인 영향을 미친다는 결과를 제시했다.
두 번째 범주인 Ghysels(2016)의 MF-VAR 모형을 이용한 연구는 크게 두 가지로 세분화할 수 있다. 먼저 전통적인 VAR 모형과 MF-VAR 모형으로 충격반응 및 분산분해 등을 측정하고 두 추정결과를 비교한 연구가 있다. 예를들어 일별로 발표되는 고빈도 자료와 월별로 발표되는 저빈도 자료를 동시에 이용하는 경우 자료의 주기가 불일치하여 분석이 불가능하다. 이 경우 자료의 주기를 통일하여 전통적인 VAR 모형을 이용하거나 자료의 주기를 통일하지 않고 MF-VAR 모형으로 변수들 간의 연관관계를 분석할 수 있는데, 이와 관련된 대표적인 연구는 Ferrara and Guérin(2018), Motegi and Sadahiro(2018), Paccagnini and Parla(2021) 등이 있다. Motegi and Sadahiro(2018)는 일본의 주식시장과 거시경제와의 연관관계를 분석하여 MF-VAR 모형 대신 전통적인 VAR 모형을 이용하는 경우 주식시장이 투자에 미치는 효과를 과소추정한다는 결과를 제시했다. Ferrara and Guérin(2018)는 미국의 금융불확실성을 대변하는 VIX 지수가 거시경제에 미치는 효과를 분석하여 불확실성 충격은 거시경제 변수들에 부정적인 충격을 주는 것으로 분석했다. 특히, 해당 월에 고빈도 자료인 불확실성 충격이 저빈도 자료인 거시경제 변수에 파급되는 충격의 단기효과는 주(week)마다 이질적으로 파급된다는 결과를 제시했다. Paccagnini and Parla (2021)는 베이지안 접근법을 MF-VAR 모형에 접목하여 미국의 VIX 충격이 거시경제에 파급되는 효과를 분석했다. 해당 연구에서도 Ferrara and Guérin(2018)와 유사하게 전통적인 VAR 및 MF-VAR 모형을 이용하여 VIX 충격이 거시경제에 미치는 충격반응을 추정했는데, 두 모형의 추정 결과는 상이한 것으로 나타났다.
Ghysels(2016)의 MF-VAR 모형을 이용한 두 번째 연구는 Diebold and Yilamz(2009, 2014)의 연계성 접근법에 MF-VAR 모형을 접목하여 시장 간 파급효과를 분석한 Cotter et al.(2023), Lv et al.(2022), Shen and Pan(2023) 등의 연구이다. Cotter et al.(2023)는 연계성 접근법에 MF-VAR 모형을 적용하는 방법을 제안하고 미국의 금융시장과 실물경제 사이의 연계성을 분석했다. Lv et al.(2022)는 중국의 금융스트레스 지수와 실물경제 간 상호의존성을 분석했으며, Shen and Pan(2023)은 중국의 상품시장과 거시경제 사이의 연관관계를 측정했다. 이 연구들은 분석시장 및 변수들이 다르지만 공통적으로 VAR 모형으로 연계성을 측정할 경우 MF-VAR 모형의 추정 결과보다 파급효과가 과소추정된다는 결론을 제시했다.
이와 같이 해외에서는 Ghysels(2016)의 MF-VAR 모형을 이용한 실증연구가 다수 진행됐으나, 국내에서는 MF-VAR 모형을 이용하여 주택시장을 분석한 연구는 여전히 제한적인 실정이다. 따라서 본 연구는 고빈도 자료인 금융불확실성지수와 저빈도 자료인 주택가격 변동률간의 연관관계를 MF-VAR 모형으로 분석하고 VAR 모형과의 추정결과를 비교한다는 점에서 본 연구의 의의가 있을 것으로 판단된다. 또한, 이와 같은 분석을 수행하여 불확실성과 주택시장의 관계를 분석한 기존문헌을 보완할 것으로 기대된다.
III. 실증분석 모형
본 연구에서 사용되는 실증분석 모형은 Ghysels(2016)의 MF-VAR 모형과 Cotter et al.(2023)의 연계성 접근법이다. 특히, 연계성 접근법은 Diebold and Yilmaz(2009, 2014)가 제안한 실증분석 모형으로 전통적인 VAR 모형에 기반하여 금융시장 간 상호연관관계를 쉽고 직관적인 방법으로 분석할 수 있는 방법으로 해당 방법론이 개발된 이후로 파급효과 분석에 널리 사용됐다.2) 그러나 분석대상 자료들의 주기가 다른 경우 고빈도 자료를 집계하여 저빈도 자료와 주기를 통일해야 하는데, 이 과정에서 고빈도 자료가 갖고 있는 정보가 손실된다. 이러한 단점을 극복하기 위해 Cotter et al.(2023)는 표본 주기가 상이한 자료 간 상호관계를 분석할 수 있는 MF-VAR 모형을 연계성 접근법에 접목했다.
먼저 K(= KH + KL) 차원의 혼합주기 시계열 과정이 존재한다고 하자. 여기서 KH 는 고빈도(금융) 자료, KL은 저빈도(거시) 자료이며 KL < K이다. 그리고 하나의 저빈도 자료가 관측되는 기간 동안 고빈도 자료는 m번 관측된다. 따라서 각각의 저빈도 자료의 기간을 m개의 그룹으로 구분하면 고빈도 자료는 <식 1>과 같이 표현할 수 있다.
여기서 KL 차원의 저빈도 주기의 시계열 자료를 KH 차원의 고빈도 주기의 시계열 자료와 결합하면 <식 2>와 같이 누적된(stacked) 벡터 로 표현할 수 있다.
<식 2>의 누적된 벡터를 Ghysels(2016)의 MF-VAR(p) 모형으로 표현하면 <식 3>과 같다.
여기서 A0 는 Kx 차원의 모수(parameter) 벡터, Aj(j=1,··· p)는 (Kx × Kx) 모수 배열(arrays), 그리고 은 Kx차원의 오차항 벡터이다. 식 (3)은 전통적인 VAR 모형과 동일한 특징을 갖고 있기 때문에 MF-VAR 모형에서도 충격반응 및 분산분해 분석을 시행할 수 있다.
Diebold and Yilmaz(2009)는 촐레스키(cholesky) 분해를 적용하여 금융시장 간 연계성을 측정했는데, j 변수의 충격이 i 변수의 h기간 예측치에 대해 영향을 미치는 비율은 <식 4>를 이용하여 계산한다.
여기서 Ah 는 MF-VAR의 이동평균 계수행렬, P는 촐레스키 인자, Σ 는 오차항 의 분산-공분산 행렬, ej는 j번째 원소만 1의 값을 갖고 j 번째 원소가 아닌 경우 0의 값을 갖는 벡터를 의미한다. 그리고 이 를 이용하면 연계성의 상대적 크기와 방향성을 고려하여 총 연계성, 방향 연계성, 순 연계성 등 다양한 연계성 지표를 도출할 수 있다.
총 연계성 지표는 분석 대상 변수의 전체 연계성을 추정하며 <식 5>와 같이 도출된다.
또한 분산분해 요소들을 이용하여 특정 변수의 연계성 방향을 파악할 수 있다. 예를들어, 변수 i 가 다른 모든 변수들에 미치는 영향을 유출 연계성, 그리고 다른 모든 변수들의 충격이 변수 i 에 미치는 영향을 유입 연계성이라 정의하며 각각 <식 6> 및 <식 7>과 같이 측정한다.
마지막으로 변수 i 가 다른 변수들에게 미친 영향과 다른 변수들로부터 받은 영향을 차감하여 유출 연계성과 유입 연계성의 차이인 순 연계성을 구한다.
여기서는 MF-VAR 모형에서 추정된 분산분해 배열들을 변환하여 전통적인 VAR 모형에서 추정된 연계성 지표들과 비교할 수 있는 Cotter et al.(2023)의 방법을 설명한다.
먼저, 변수가 두 개인데 한 변수는 월별로 관측되는 자료이고 다른 한 변수는 주(week)마다 관측되어 MF-VAR 모형을 이용할 경우 두 시계열은 로 구성된 (5 × 1) 벡터 과정이 된다.3) 한편, 해당 자료들을 전통적인 VAR 모형으로 분석하기 위해서는 고빈도 자료를 집계하여 저빈도 자료의 주기와 맞춰야 한다. 이 경우 로 구성된 (2 × 1) 벡터 과정이 된다. 여기서 xHtL(τL)는 고빈도 주기의 자료를 저빈도 주기의 자료로 변환한 시계열 자료이다. 따라서 MF-VAR 모형과 전통적인 VAR 모형의 분산분해 배열의 차원은 <식 8>과 같이 각각 (5 × 5), (2 × 1)이 된다.
그리고 혼합주기 VAR 모형의 분산분해 배열은 <식 9>와 같은 부분(sub) 배열로 구성된다.
여기서
<식 9>의 분산분해의 부분 배열 은 <식 8>의 전통적인 VAR 모형의 분산분해 배열 에 대응한다. 즉, Cotter et al.(2023)는 MF-VAR 모형에서 추정된 분산분해 요소의 배열을 전통적인 VAR 모형의 분산분해 배열과 동일한 구조를 갖는 변환 방법을 제안했으며, 이를 로 표현하고 <식 10>과 같이 계산한다.
여기서 와 는 각각 <식 4>의 분자와 분모를 의미하며, Ik와 Jl는 각각 <식 10>의 행과 열의 지수(index)를 포함하는 집합이다.
앞에서 설명한 월별 및 주별 주기의 자료로 구성된 2변수 예에서 k= 1, l = 1인 경우 I1 = {1,…, 4}, J1 = {1, …, 4}이고 ( 원소)는 <식 11>과 같이 계산한다.
유사하게 k = 2, l = 1인 경우 I2 = {5}, J1 = {1, …, 4}이고 ( 원소)은 <식 12>와 같이 계산한다.
Ⅳ. 분석자료 및 실증분석 결과
본 연구는 일별로 발표되는 VKOSPI 지수, 그리고 월별로 발표되는 아파트 매매가격지수 및 전세가격지수를 이용한다. VKOSPI 지수는 2003년 1월부터 자료를 제공하며 해당 자료는 KRX(한국거래소) 「정보데이터시스템」에서 취득했다. 주택가격지수는 국민은행에서 발표하는 「주택가격동향조사」에서 얻었으며 X-12 ARIMA 방법론을 이용하여 계절조정을 시행했다. 분석기간은 2003년 1월부터 2022년 12월까지이다.
먼저, 전통적인 VAR 모형을 이용하는 경우 고빈도 자료를 저빈도 자료의 주기와 통일하기 위해 일별로 관측된 VKOSPI 지수를 매월마다 평균하여 월별 자료로 변환했다. 그리고 혼합주기 VAR 모형을 이용하는 경우 실증분석에서 균형된 자료를 얻기 위해 일별로 관측되는 VKOSPI 지수가 매월 고정된 4개의 주(week)가 있는 것으로 가정했다. 즉, 일별로 관측된 VKOSPI 지수를 재구성하여 매월 4개의 주로 구성된 주별 자료로 변환했는데, 이를 위해 Ferrara and Guérin(2018)에서 사용한 방법을 이용했다. 구체적으로 Dt는 t월에 관측된 거래일수를 뜻하며, 일별로 관측된 고빈도 자료로부터 다음과 같이 주별 자료를 얻는다. 먼저 첫째 주의 기간은 첫번째 거래일부터 Dt - 15일까지, 둘째 주의 기간은 Dt - 14일부터 Dt - 10일까지, 셋째 주의 기간은 Dt - 9일부터 Dt - 5일까지, 넷째 주의 기간은 Dt - 4일부터 Dt 까지로 한다. 그리고 각 주의 마지막 관측치를 주별 자료로 사용한다. 즉 Dt - 15일, Dt - 10일, Dt - 5일, Dt 일 자료가 각각 VKOSPI1 (첫째 주), VKOSPI2(둘째 주), VKOSPI3(셋째 주), VKOSPI4(넷째 주)에 해당하는 금융불확실성 자료에 해당된다.
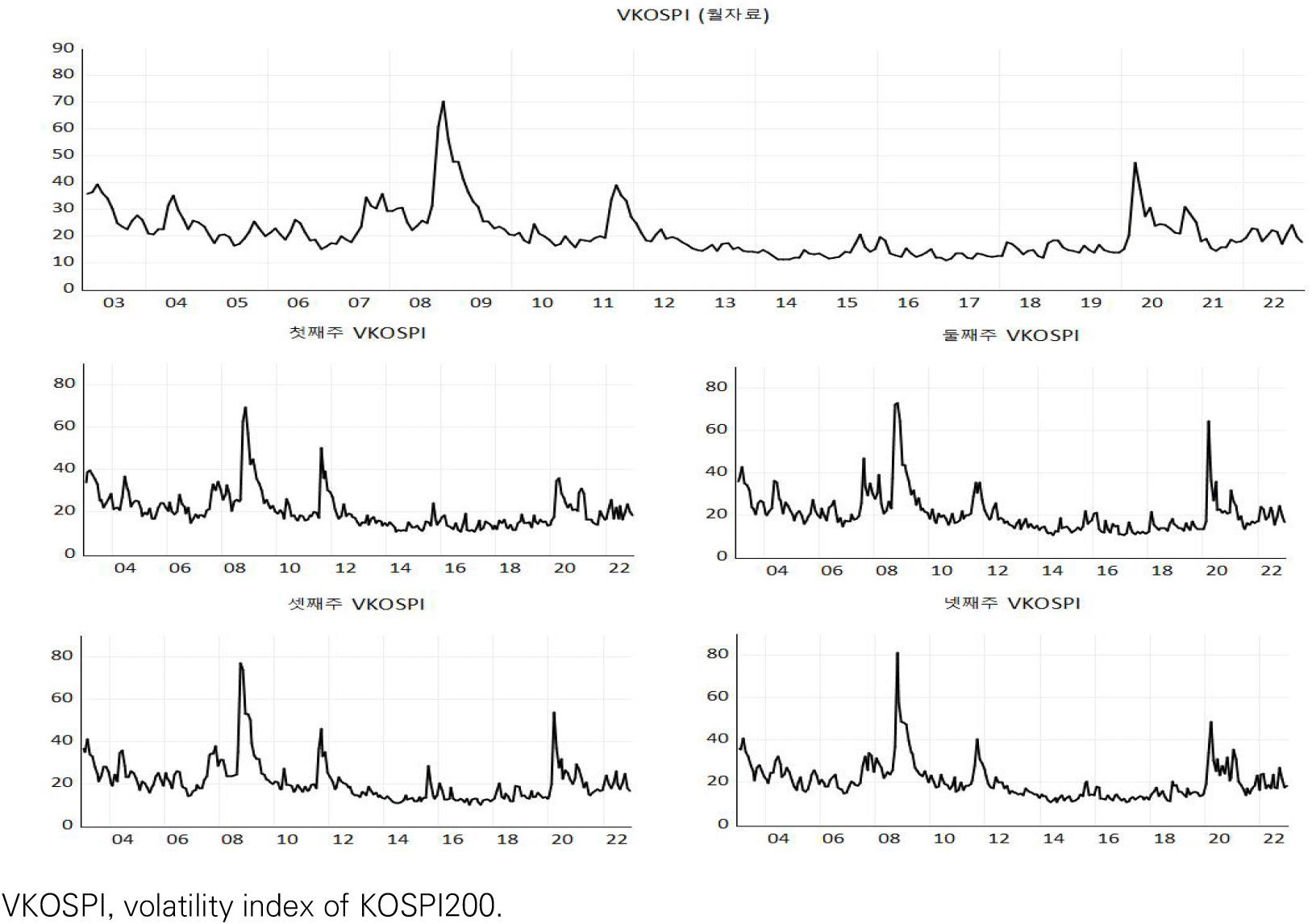
<그림 1>은 월간 VKOSPI 자료와 4개의 주로 구성된 VKOSPI 자료를 제시했다. 월간 자료를 중심으로 금융불확실성 지수의 특징을 살펴보면 경제위기가 발생한 시기에 VKOSPI 지수가 상승하는 것을 볼 수 있는데, 대표적으로 2007~2009년 글로벌 금융위기, 2010년 하반기부터 부각된 유럽재정위기, 그리고 2020년부터 시작된 코로나19 사태 등의 기간에 해당 지수가 상승했다. 그리고 월간 VKOSPI 지수 아래에는 주별 자료로 구성된 VKOSPI 지수(VKOSPI1, VKOSPI2, VKOSPI3, VKOSPI4)를 제시했는데, 기본적으로 주별 자료도 경제위기 기간에 모두 상승하며 유사한 패턴을 갖는 것을 볼 수 있지만, 주별로 불확실성의 크기가 약간씩 차이가 있는 것을 확인할 수 있다.
다음으로 분석대상 자료의 단위근 검정결과는 <표 1>에 제시했다. 여기서는 ADF(Argmented Dickey-Fuller) 검정과 PP(Phillps-Perron) 검정결과를 제시했으며, 주택시장 변수인 아파트 매매가격과 전세가격은 수준변수와 로그 차분 후 100을 곱한 변화율 자료를 대상으로 단위근 검정을 시행했다. 분석결과를 살펴보면 주택매매가격 및 전세가격지수에서는 단위근이 존재하는 것으로 나타났지만 월간 및 주간 VKOSPI 지수, 그리고 주택가격 변화율 자료는 모두 5% 유의수준에서 단위근이 존재한다는 귀무가설을 기각하여 단위근이 존재하지 않는 안정적인 시계열 자료로 나타났다.
<표 2>에는 주요 변수의 기초통계량을 제시했다. 먼저 VKOSPI 자료를 살펴보면 월간 자료와 달리 주별 VKOSPI 지수의 기초통계량은 주별로 이질적인 특징을 보인다. 구체적으로, 첫째 주 VKOSPI를 뜻하는 VKOSPI1 자료부터 넷째 주 VKOSPI4 자료의 평균, 중앙값, 최댓값, 최솟값, 표준편차 등의 통계량은 약간씩 상이한 특징을 보이는데, 이와 같은 특징은 일별 자료를 집계한 월간 자료(VKOSPI)에서는 나타나지 않는 특징이다. 그리고 아파트 매매가격 및 전세가격 변화율의 월평균은 0.34%, 0.32%로 각각 추정되어 분석대상 기간 동안 평균적으로 주택시장은 상승한 것으로 나타났다. 추가적으로 분석 대상 변수들의 왜도와 첨도 통계량을 보면 경제시계열 자료가 갖는 정형화된 특징(비대칭·과첨 분포) 과 유사한 특징을 보인다.
VKOSPI, volatility index of KOSPI200.
본절에서는 금융불확실성이 주택시장에 미치는 파급효과를 분석한다. 먼저 일별 VKOSPI 자료를 주택가격 변화율 자료와 자료의 주기를 일치시키기 위해 월간 자료로 집계한 다음 VAR 모형으로 충격반응 및 분산분해 분석을 시행한다. 다음으로 MF-VAR 모형을 이용하여 동일한 분석을 시행하고 VAR 모형과 MF-VAR 모형의 추정결과를 비교·분석한다. 충격반응 및 분산분해 분석을 시행할 때 두 모형 모두 촐레스키 분해를 이용했으며, 거시경제 요인을 통제하기 위해 산업생산지수, 소비자물가지수, CD금리를 안정적인 시계열로 변환 후 분석모형에 외생변수로 포함했다.4) 그리고 VAR 및 MF-VAR 모형의 시차는 SC 기준에서 1을 선택했다.
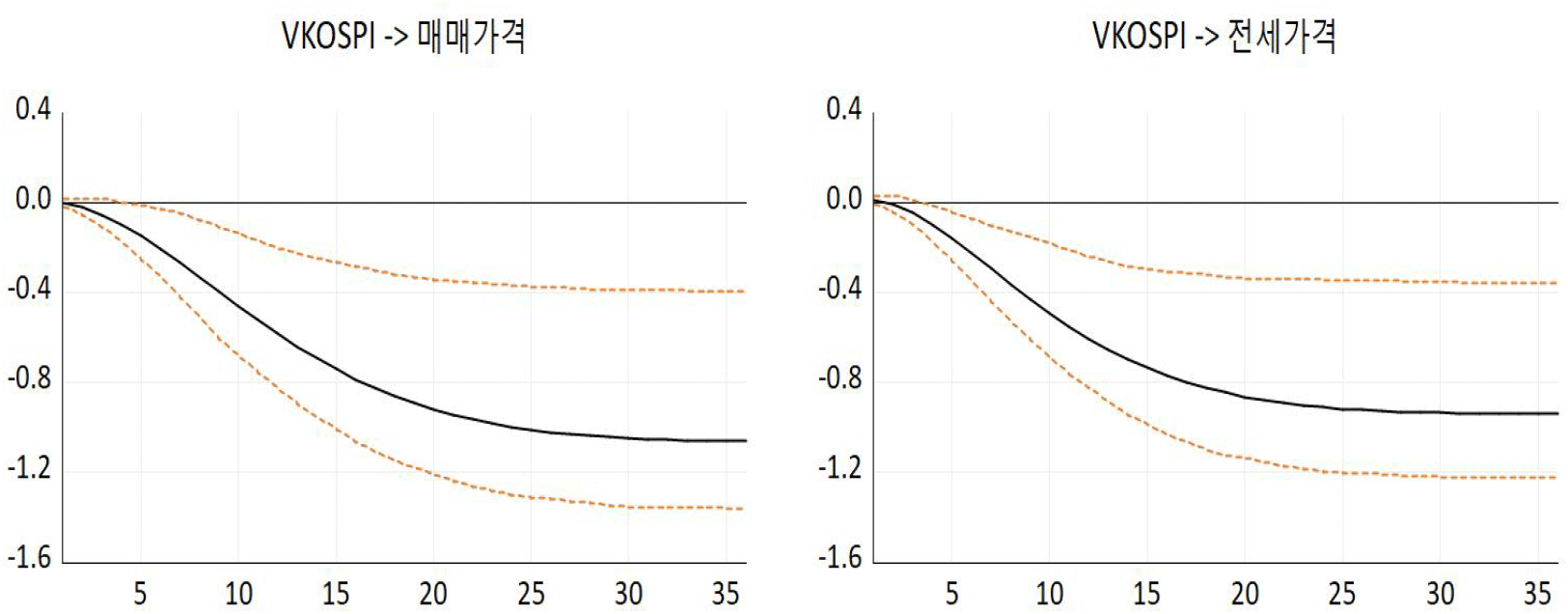
<그림 2>는 금융불확실성(VKOSPI)이 1 표준편차 만큼 증가할 때 주택시장에 파급되는 누적충격반응함수 결과를 제시했다. 촐레스키 분해를 적용할 때 변수의 순서는 VKOSPI, 아파트매매가격 변동률, 아파트전세가격 변동률 순서로 배열했으며, 누적충격반응의 68% 신뢰구간은 부트스트랩을 999회 이용하여 도출했다. 분석결과를 살펴보면 금융불확실성이 상승하면 아파트매매가격 및 전세가격이 하락하는 것으로 분석됐다. 이러한 결과는 경제정책 불확실성지수(economic policy uncertainty, EPU)가 상승하면 매매가격에 음의 효과를 미친다는 결과를 제시한 김지연 외(2020)의 결과와 유사한 것으로 나타났다.
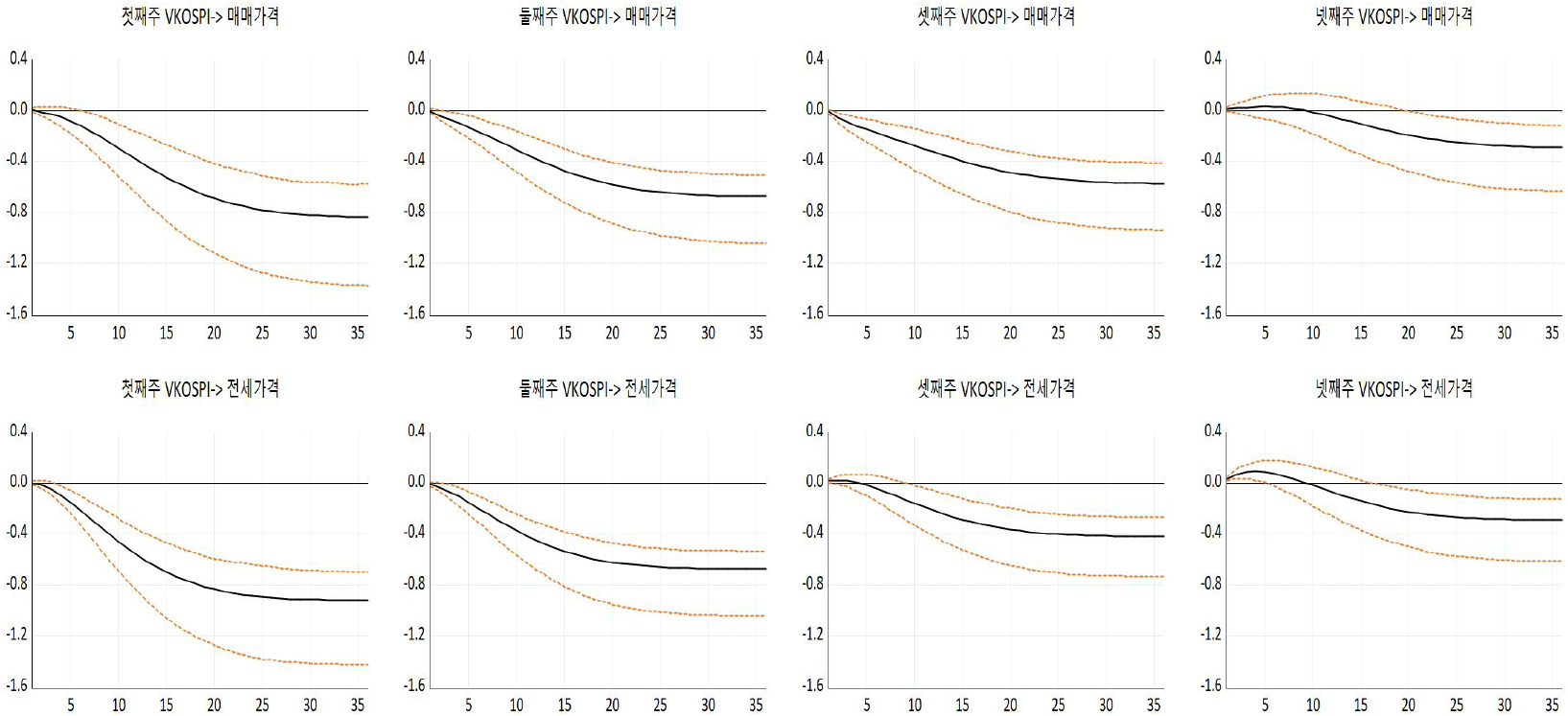
다음으로 MF-VAR 모형을 이용하여 금융불확실성이 주택시장에 미치는 영향을 분석한다. 충격반응함수를 추정할 때 변수의 순서는 VKOSPI1, VKOSPI2, VKOSPI3, VKOSPI4, 아파트매매가격, 아파트전세가격 순으로 배열했다. 일반적으로 변수의 배열에 대한 논리적 또는 실증적 근거가 없는 경우 Pesaran and Shin(1998)의 일반화 충격반응함수를 적용할 수 있으나, 여기서는 Ghysels(2016), Ferrara and Guérin(2018)에서 분석한 것과 동일하게 해당 자료가 발표되는 발표일과 발표시차를 고려하여 변수를 배열했다. 구체적으로 둘째 주의 금융불확실성 자료 VKOSPI2는 첫째 주의 VKOSPI1이 발표되기 전에는 관측되지 않으므로 VKOSPI1 뒤에 배열했으며, VKOSPI3, VKOSPI4도 유사하게 발표일 순서대로 배열했다. 그리고 국민은행에서 제공하는 월간 아파트 매매 및 전세가격지수의 통계자료 발표일은 매 조사 기준 월말 혹은 익월 초에 발표된다. 따라서 해당자료는 발표시차가 존재하여 VKOSPI4 뒤에 배열했다.
<그림 3>은 MF-VAR 모형을 적용하여 추정한 충격반응함수 결과이다.5) 분석결과를 살펴보면 각 주마다 1 표준편차 만큼의 VKOSPI 상승 충격이 발생하면 아파트매매가격 및 전세가격은 하락하는 것으로 나타났다. 특히, 금융불확실성이 주택시장에 파급되는 충격의 효과는 VKOSPI의 발표시차에 따라 이질적인 것을 확인할 수 있다.
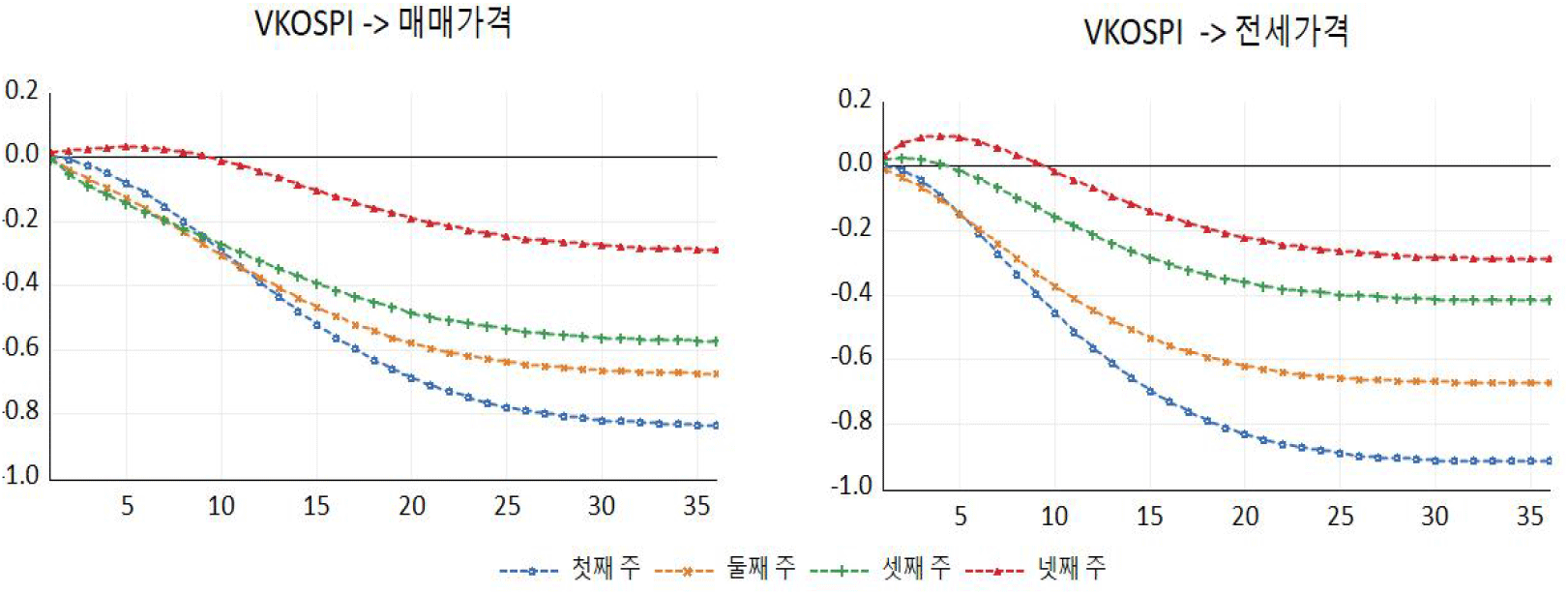
VAR 및 MF-VAR 모형을 이용하여 VKOSPI 지수가 주택시장에 미치는 분산분해분석은 <표 3> 및 <표 4>에 각각 정리했다. 먼저 전통적인 VAR 모형의 추정결과를 제시한 <표 3>을 살펴보면 예측오차 기간이 길어길수록 VKOSPI 지수가 매매가격 및 전세가격에 파급되는 효과가 증가하는 것으로 나타났다. 구체적으로 VKOSPI가 매매가격에 미치는 비중은 6개월 뒤 2.45% 비중을 차지한 반면, 36개월 뒤에는 9.76%로 매매가격의 변동에서 차지하는 비중이 증가했다. 전세가격의 경우에도 이와 유사하게 시간이 지남에 따라 VKOSPI의 영향력이 점차 증가하며, 특정 값으로 수렴하는 것으로 나타났다.
VAR, vector autoregressive; VKOSPI, volatility index of KOSPI200.
MF-VAR, mixed frequency vector autoregressive; VKOSPI, volatility index of KOSPI200.
MF-VAR 모형으로 불확실성이 주택시장에 파급되는 분산분해 결과는 <표 4>에 정리했다. 분석결과를 살펴보면 VAR 모형의 결과와 유사하게 시간이 지날수록 VKOSPI의 영향력이 증대되는 것으로 나타났는데, 여기서는 추가적으로 주별로 주택시장에 미치는 파급효과를 파악할 수 있다. 구체적으로 36개월 뒤 VKOSPI1, VKOSPI2, VKOSPI3, VKOSPI4가 각각 매매가격의 변동을 설명하는 비중은 5.64%, 3.63%, 2.61%, 0.93%로 측정됐으며, 충격반응함수의 결과와 유사하게 첫째 주의 불확실성 충격의 효과가 다른 주의 불확실성 효과보다 큰 것으로 분석됐다. 이러한 결과는 시간표(time-stamped)상의 효과를 반영하며, 두 모형의 추정결과를 비교해보면 불확실성 충격이 주택시장에 미치는 효과는 VAR 모형이 MF-VAR 모형보다 작은것으로 나타났다. 예를들어, <표 3>에서 VKOSPI가 매매가격의 변동을 설명하는 비중은 9.76%인 반면, MF-VAR 모형을 이용한 경우 총 효과는 11.29%로 추정됐다. 이는 VAR 모형이 MF-VAR 모형과 비교하여 분산분해의 영향력을 과소추정하는 것으로 분석한 Motegi and Sadahiro(2018)의 결과와 유사한 것으로 분석됐는데, 이러한 결과는 일별 자료를 월별자료로 집계하는 과정에서 정보의 손실이 발생하여 나타난 결과로 해석된다.
여기서는 앞에서 도출한 분산분해 결과를 이용하여 금융불확실성과 주택시장 간 연계성 분석을 시행한다. <표 5>는 2003년 2월부터 2022년 12월까지 금융불확실성과 주택시장 사이의 연계성을 추정한 결과이다. 해당 결과는 <표 3> 및 <표 4>의 분산분해 결과를 토대로 정리했는데, <표 5>의 panel (a)는 VAR 모형에 기반한 Diebold and Yilmaz(2009, 2014)의 연계성 접근법을 이용한 추정결과이며 panel (b)는 Cotter et al.(2023)의 MF-VAR 모형에 기반한 추정결과이다. 추정결과를 정리할 때 분산분해 기간은 12개월(1년)로 설정했다.
<표 5>에서 주요 특징을 살펴보면 금융불확실성은 주택시장에 영향을 끼치는 것으로 분석됐는데, 전반적으로 전통적인 VAR 모형이 MF-VAR 모형보다 금융불확실성과 주택시장 사이의 연관관계를 과소추정하는 것으로 나타났다. 구체적으로 VAR 모형을 이용한 Panel (a)의 결과에서 시장 전체의 연관관계를 하나의 숫자로 표현한 총 연계성은 18.39%로 측정된 반면, MF-VAR 모형을 이용한 Panel (b)에서는 20.51%로 측정됐다. 또한 금융불확실성을 의미하는 VKOSPI가 주택시장에 파급되는 영향력을 측정한 유출 연계성은 VAR 모형에서 16.21%로 추정됐으며, MF-VAR 모형에서는 23.65%로 측정됐다. 반대로 VKOSPI가 주택시장으로부터 받는 영향력인 유입 연계성은 VAR 모형에서 1.78%, MF-VAR 모형에서는 1.42%로 추정됐는데, 주택시장으로부터 받는 영향력은 매우 작게 나타났다. 마지막으로 VKOSPI의 순 영향력을 측정하는 순 연계성(=유출–유입)은 VAR 모형에서 14.43%(=16.21%–1.78%), MF-VAR 모형에서는 22.23%(=23.65%–1.42%)로 측정되어 일별 자료를 월별 자료로 변환한 전통적인 VAR 모형의 추정결과가 MF-VAR 모형보다 파급효과를 과소추정하는 것을 확인할 수 있다.
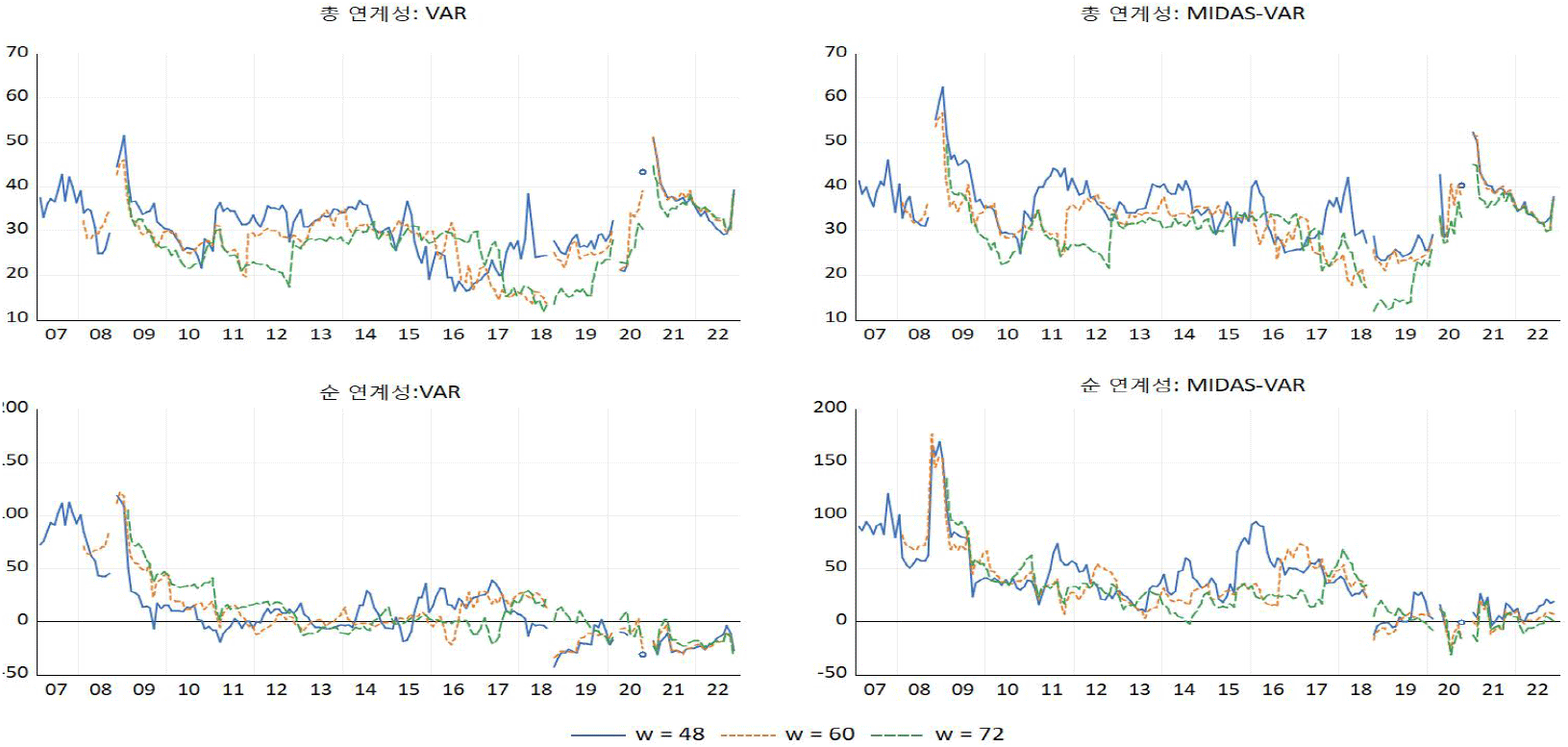
다음으로 <그림 4>에서는 표본이동분석을 이용하여 총 연계성의 시간가변 추이를 제시했다. 표본이동의 이동폭은 선행연구인 Cotter et al.(2023)와 동일하게 60개월(5년)로 설정했다.6) 분석결과를 살펴보면 VAR 및 MF-VAR 모형에서 추정된 총 연계성의 패턴은 전반적으로 유사한 것으로 나타났다. 특히, 경제상황에 따라 총 연계성은 변동하며 위기 기간에 총 연계성은 상승하는 것으로 나타났는데, 2007~2009년 글로벌 금융위기나 2020년 코로나19 팬데믹 등 경제위기 시기에 총 연계성이 상승하는 것을 볼 수 있다. 그러나 총 연계성의 크기는 <표 5>의 정태적 분석과 동일하게 VAR 모형보다는 MF-VAR 모형의 총 연계성이 더 큰 것으로 나타났다. 구체적으로 VAR 모형을 이용하여 추정된 총 연계성 지수의 평균은 28.35%이고 MF-VAR 모형을 이용하여 추정된 총 연계성 지수의 평균은 32.17%로 추정되어 월별 자료를 이용한 VAR 모형 보다는 MF-VAR 모형의 총 연계성이 평균적으로 약 4%포인트 정도 높게 나타났다. 이러한 결과는 일별자료를 월별자료로 집계하는 과정에서 정보의 손실이 발생하여 나타난 결과로 볼 수 있으며, 해당 결과는 미국의 금융시장과 실물경제 간 연관관계를 VAR과 MF-VAR 모형으로 비교 분석한 Cotter et al.(2023)의 결과와 유사한 것으로 나타났다. <그림 5>는 금융불확실성이 주택시장에 미치는 순 연계성을 제시한 그림인데, 여기서도 총 연계성 지수의 결과와 유사하게 두 지수의 패턴은 유사하지만 VAR 모형의 순 연계성은 MF-VAR 모형의 순 연계성보다 과소 추정된 것으로 나타났다. 특히, 금융불확실성은 2008년 글로벌 금융위기 시기에 주택시장에 큰 영향을 끼쳤던 것으로 나타났다. 그 이후 순 연계성은 점진적으로 감소하다 2016년 전후로 다시 상승한 것을 볼 수 있는데, 이는 해당 시기에 대외경제 불안 증가 및 미국 금리 인상 등으로 금융불확실성이 주택시장에 미치는 영향력이 확대된 것으로 해석된다.
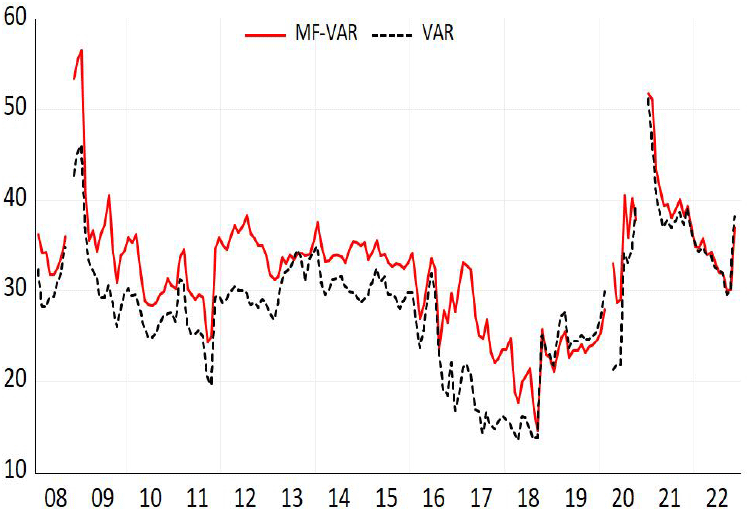
VAR, vector autoregressive; MF-VAR, mixed frequency vector autoregressive; VKOSPI, volatility index of KOSPI200.
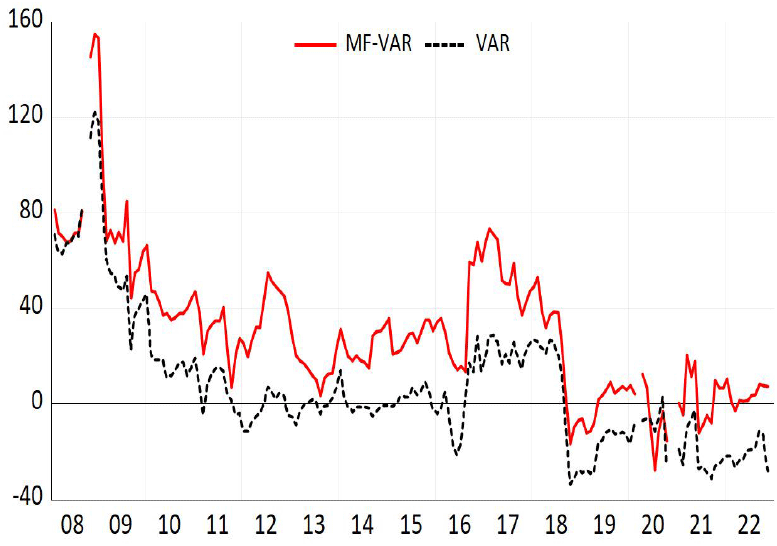
앞절에서는 금융불확실성과 전국 주택시장을 대상으로 연계성 분석을 시행했는데, 여기서는 김지연 외(2020)와 유사하게 주택시장을 세분화하여 분석을 시도한다. 즉, 전국을 수도권(서울, 경기, 인천), 5대광역시(부산, 대구, 대전, 광주, 울산), 지방(수도권과 광역시 제외) 권역으로 구분한 다음 금융불확실성과 권역별 주택시장의 상호의존성을 분석한다. 국민은행 주택가격동향조사에서 권역별 아파트지수를 2003년 9월부터 발표하여 분석기간은 2003년 9월부터 2022년 12월지로 설정했다. VAR 및 MF-VAR 모형의 시차는 SC기준에서 시차 1을 선정했으며 촐레스키 분해를 적용할 때 변수의 순서는 VKOSPI(VKOSPI1, VKOSPI2, VKOSP3, VKOSPI4), 수도권, 5대광역시, 지방도시 순으로 배열했다. 여기서 아파트가격의 배열순서는 주택가격의 파급은 경제 중심지역에서 주변지역으로 확산된다는 기존의 실증분석 결과를 고려하여 배열했다.
<표 6>은 금융불확실성과 권역별 주택시장의 연계성을 정리한 결과이다.7) 금융불확실성과 권역별 매매시장의 연계성을 측정한 Panel (a)를 살펴보자. 여기서도 금융불확실성은 권역별 매매시장에 영향을 미치는 것을 파악할 수 있는데, VAR 모형의 추정결과는 MF-VAR 모형의 추정결과보다 금융불확실성과 주택시장의 연계성을 과소추정하는 것을 확인할 수 있다. 구체적으로 MF-VAR 모형의 총 연계성은 30.59%인 반면, VAR 모형의 총 연계성은 28.70%으로 약간 과소추정됐다. 마찬가지로 MF-VAR 모형의 유출 및 순 연계성은 22.59%, 18.87%로 측정됐는데, VAR 모형에서는 16.15%, 13.66%로 나타나 MF-VAR 모형보다 작게 추정된 것을 확인할 수 있다. 한편, <표 6> Panel (a)의 총 연계성은 <표 5>의 총 연계성 추정결과보다 더 높게 나타났는데, 이는 VAR 모형에 포함된 변수의 수가 증가하면 연계성이 증가하기 때문에 나타난 현상으로 볼 수 있다.
VAR, vector autoregressive; MF-VAR, Mixed frequency vector autoregressive.
다음으로 금융불확실성과 권역별 전세시장의 연계성을 측정한 Panel (b)를 살펴보자. 여기서도 Panel (a)와 유사하게 금융불확실성은 주택시장에 영향을 미치지만 VAR 모형은 MF-VAR 모형의 추정결과보다 해당 영향력을 과소추정하는 것을 알 수 있다. 한편, Panel (b)에서 총 연계성은 Panel (a)의 총 연계성보다 더 높은 것으로 나타났는데 이는 매매시장보다는 전세시장 사이의 상호의존성이 더 높다는 것을 의미한다. 이러한 결과는 지역별 매매시장과 전세시장의 상호의존성을 각각 분석하고 매매시장 사이의 연계성보다 전세시장 사이의 연계성이 더 높게 추정된 Al-Yahyaee et al. (2021)의 결과와 유사한 것으로 나타났다.
<그림 6>은 표본이동분석(60개월)을 이용하여 금융불확실성과 권역별 주택시장의 총 연계성 추이를 제시했다. <그림 6>에서도 전반적으로 VAR 모형보다 MF-VAR 모형에서 추정된 총 연계성이 더 크게 측정됐으며, 공통적으로 글로벌 금융위기나 코로나19 등의 경제위기가 발생한 시기에 총 연계성이 상승하는 것으로 나타났다. 그리고 정태적 분석결과와 유사하게 금융불확실성과 매매시장의 총 연계성보다는 금융불확실성과 전세시장의 총 연계성이 약간 더 높게 추정됐다.
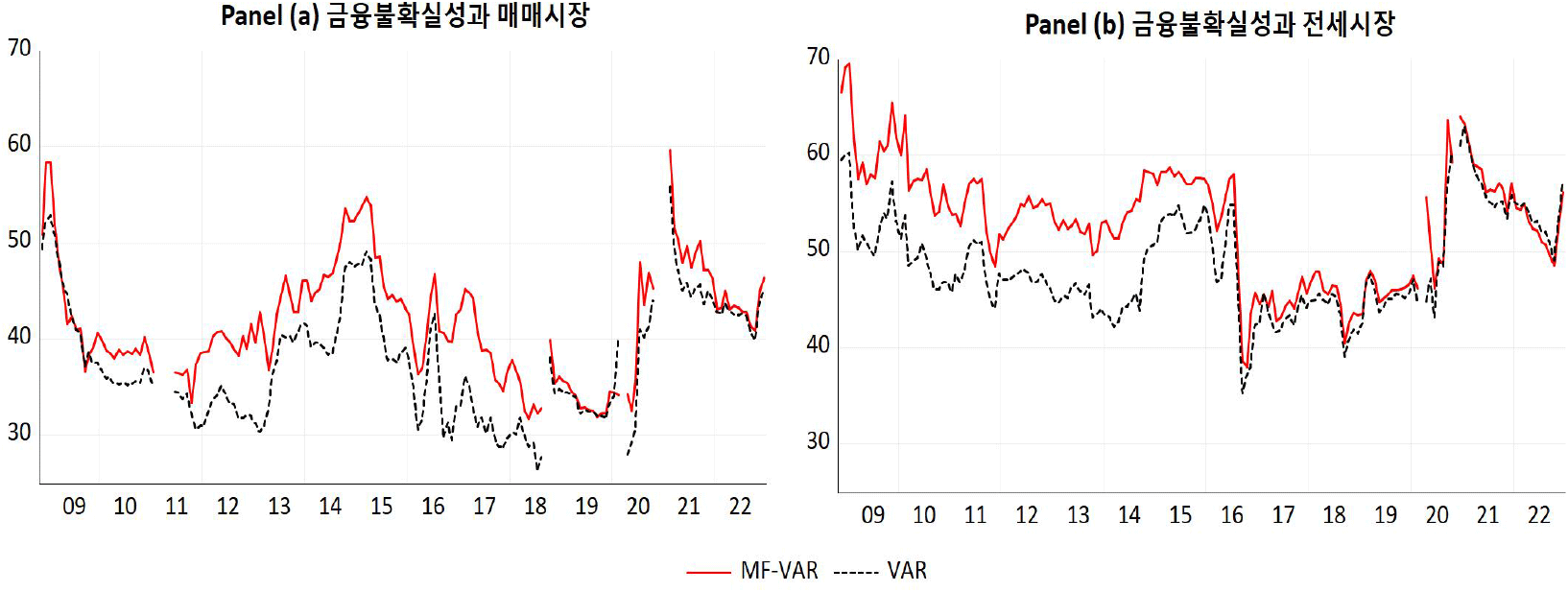
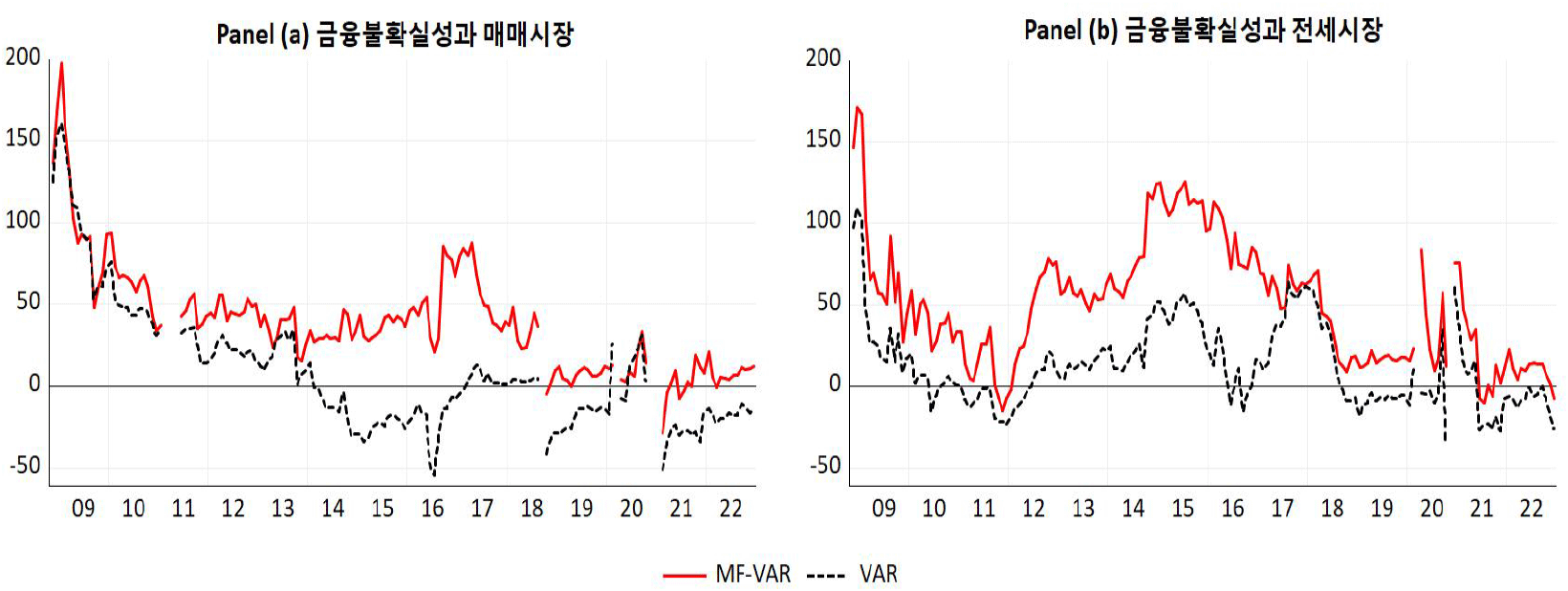
<그림 7>에서는 금융불확실성의 순 연계성 추정결과를 제시했다. <그림 5>의 순 연계성 추이와 유사하게 글로벌 금융위기 기간 및 2016년 전후 시기에 불확실성이 주택시장에 미치는 영향력이 상승하는 것을 볼 수 있다. 그리고 금융불확실성은 매매시장보다는 전세시장에 미치는 영향력이 약간 더 큰 것으로 나타났는데, 이와 관련해서는 추가적인 연구가 필요한 것으로 판단된다.
V. 결론
본 연구는 불확실성과 주택시장 사이의 연계성을 분석했다. 특히 Baker et al.(2016)의 불확실성지수(EPU)를 이용한 기존 연구들과 달리 고빈도 자료인 변동성지수(VKOSPI)를 불확실성의 대리변수로 이용하여 불확실성이 주택시장에 미치는 영향을 분석했다. 이 경우 고빈도 자료인 VKOSPI 지수와 주택가격지수는 자료의 주기가 서로 불일치한 문제가 발생하는데, 이 부분은 Ghysels(2016)의 MF-VAR 모형을 이용하여 해결했다. 표본기간은 2003년 1월부터 2022년 12월까지이며, 금융불확실성이 주택시장에 미치는 효과를 MF-VAR 모형과 전통적인 VAR 모형을 이용하여 각각 추정하고 해당 추정결과를 비교·분석했다.
주요실증분석 결과는 다음과 같다. 첫째, 충격반응함수 추정결과 금융불확실성이 상승하면 아파트매매가격 및 전세가격은 하락하는 것으로 나타났다. 특히, MF-VAR 모형에서 금융불확실성이 주택시장에 파급되는 효과는 충격이 발생한 시점별로 이질적으로 나타났다. 둘째, 분산분해 분석결과 금융불확실성은 주택시장에 영향을 미치는 것으로 나타났으며, 전통적인 VAR 모형은 MF-VAR 모형보다 금융불확실성이 주택시장에 미치는 영향력을 과소추정하는 것으로 나타났다. 셋째, MF-VAR 모형에 기반한 Cotter et al.(2023)의 연계성 접근법을 이용한 결과 금융불확실성은 아파트매매가격 및 전세가격변화율에 영향을 끼치는 것으로 나타났다. 특히, 해당 영향력은 지방보다는 수도권 및 5대광역시에 미치는 효과가 더 큰 것으로 분석됐다. 넷째, 연계성 접근법에 기초한 표본이동분석결과 금융불확실성과 주택시장의 연계성은 글로벌 금융위기 및 코로나19 등 경제위기 기간에 높아지는 것으로 분석됐으며, 금융불확실성은 주택시장에 지속적으로 영향을 미치는 순 전달자 역할을 하는 것으로 나타났다.
본 연구는 전통적인 VAR 모형 및 MF-VAR 모형으로 금융불확실성과 주택시장의 연계성을 추정하고 추정결과를 비교했는데, 전통적인 VAR 모형은 불확실성이 주택시장에 미치는 영향력을 전반적으로 과소추정하는 것으로 확인했다. 이러한 결과는 일별 자료를 월별 자료로 변환하는 과정에서 발생하는 정보의 손실이 발생하여 변수들 간의 상호작용을 세밀하게 포착하지 못한다는 것을 의미한다. 즉 고빈도 자료에서 나타나는 변화가 주택시장에 미치는 영향을 충분히 포착하지 못해 금융불확실성의 영향력을 과소평가하는 결과가 나타나는데, 이는 정책 당국자에게 잘못된 신호를 제공하여 부정확한 정책 대응을 초래할 가능성이 있다. 따라서 자료 간의 불일치가 발생하는 경우 가급적 정보의 손실을 최소화할 수 있는 모형을 이용하여 분석을 시행할 필요가 있다.
본 연구에서는 자료 간의 불일치가 발생하는 경우 MF-VAR 모형을 이용하여 금융불확실성이 주택시장에 파급되는 효과를 실증분석하는데 의의가 있다. 그러나 자유도 감소 문제로 불확실성이 주택시장에 미치는 효과를 전국 및 대권역(수도권, 5대광역시, 지방)으로 분류하여 분석한 한계점이 존재하는데, 추후 연구에서는 지역별로 분석을 시도할 필요가 있다. 또한, 금융불확실성이 높은 시기와 낮은 시기에 불확실성이 주택시장에 파급되는 효과를 구분하지 못한점에서 한계를 갖는데, 이러한 부분은 후속연구에서 다루기로 한다. 마지막으로 본 연구는 금융불확실성의 대리변수로 VKOSPI 지수를 선정하여 금융불확실성이 주택시장에 미치는 영향을 살펴봤는데, 불확실성에 대한 대리변수의 설정에 따라 분석결과가 상이할 가능성이 존재한다. 따라서 향후에는 외생적 불확실성을 반영할 수 있는 지표를 대리변수로 이용하여 이에 대한 연구를 지속할 필요가 있다.